信创网安wp

ctf > 赛题复现wp

发布时间 : 2022-12-05 10:42

阅读 :

RevShift
ReContract

easy_Affline

gauss_system

省排名：22

web师傅纠结于web最后一题，所以杂项一道没做。然后我把仿射密码的做题思路给忘了，然后密码0解，至于pwn….

RevShift

str1='≁⧃⩆㷕⿤ᩣᡤ㋟㩨ᣳ⿃ᣰ㑥㥟⫴㍽'
print(str1)
for i in str1:
    t = ord(i)&0xff
    if t > 128:
        print(chr(ord(i) >> 7)+chr((ord(i)-128)&0xff),end='')
    else:
        print(chr(ord(i) >> 7)+chr((ord(i))&0xff),end='')

f.close()
print(int('10000000',2))
# DASCTF{U_d4c0de_th1s_C1pher_Utf}

ReContract

1.智能合约的题，我也是第一次做，但提示说是一道容易题，查看文件发现前面有几个数字缺了，直接百度搜着找就行

2.然后又找到一篇文章，上面写着一个在线工具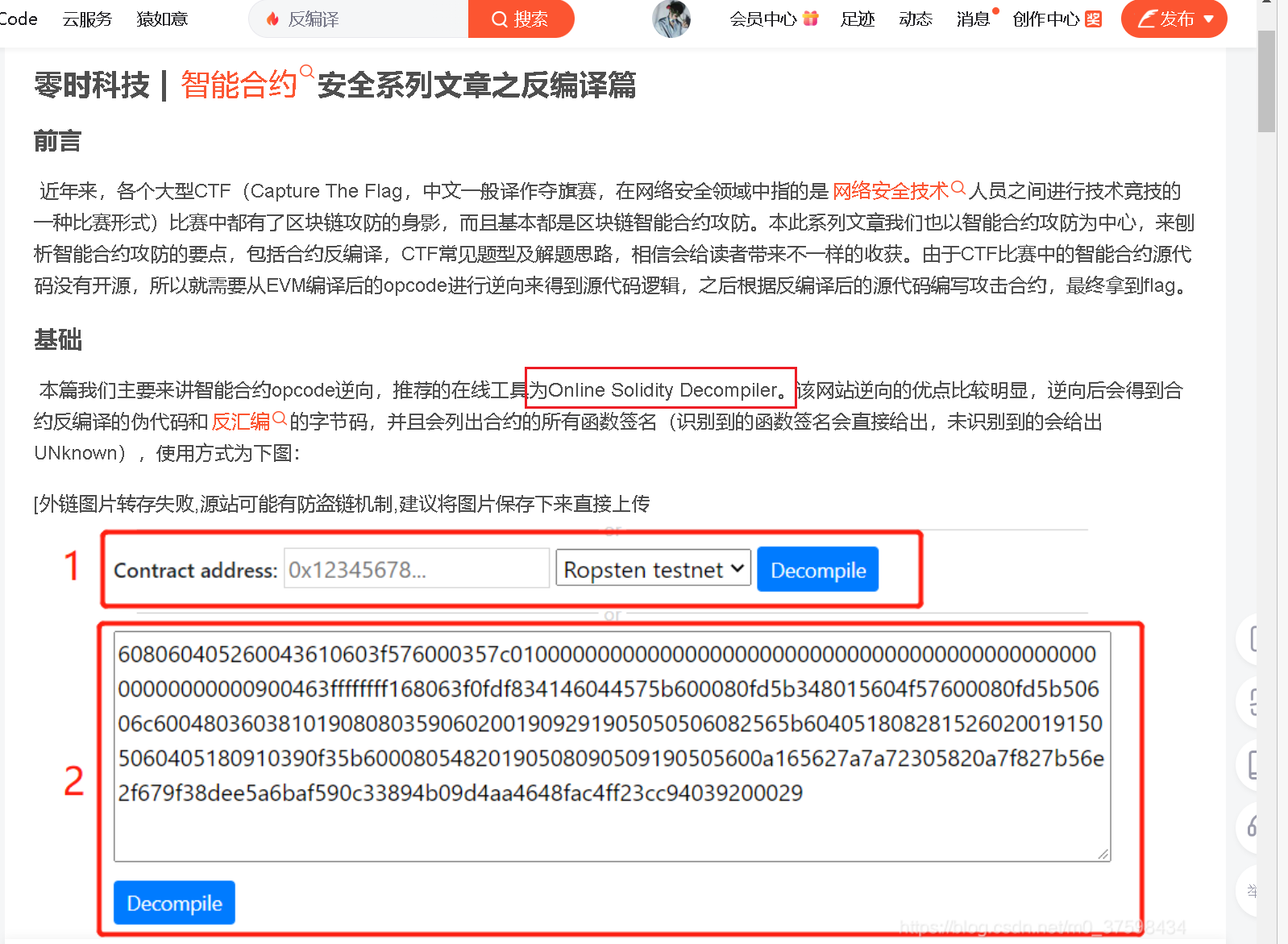

3.直接将字节码复制进去翻译即可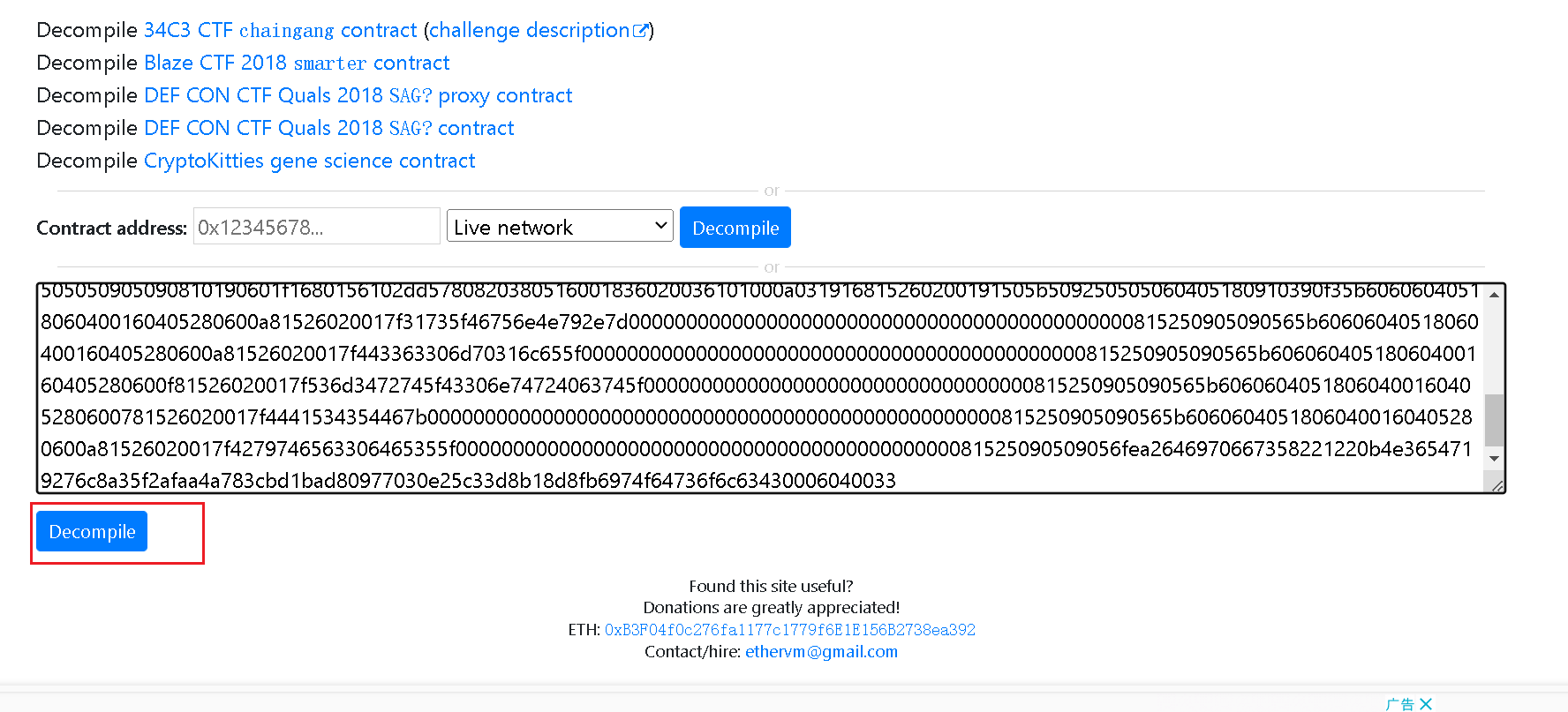

4.这里看见有五个可疑数字，拿去转字符串看看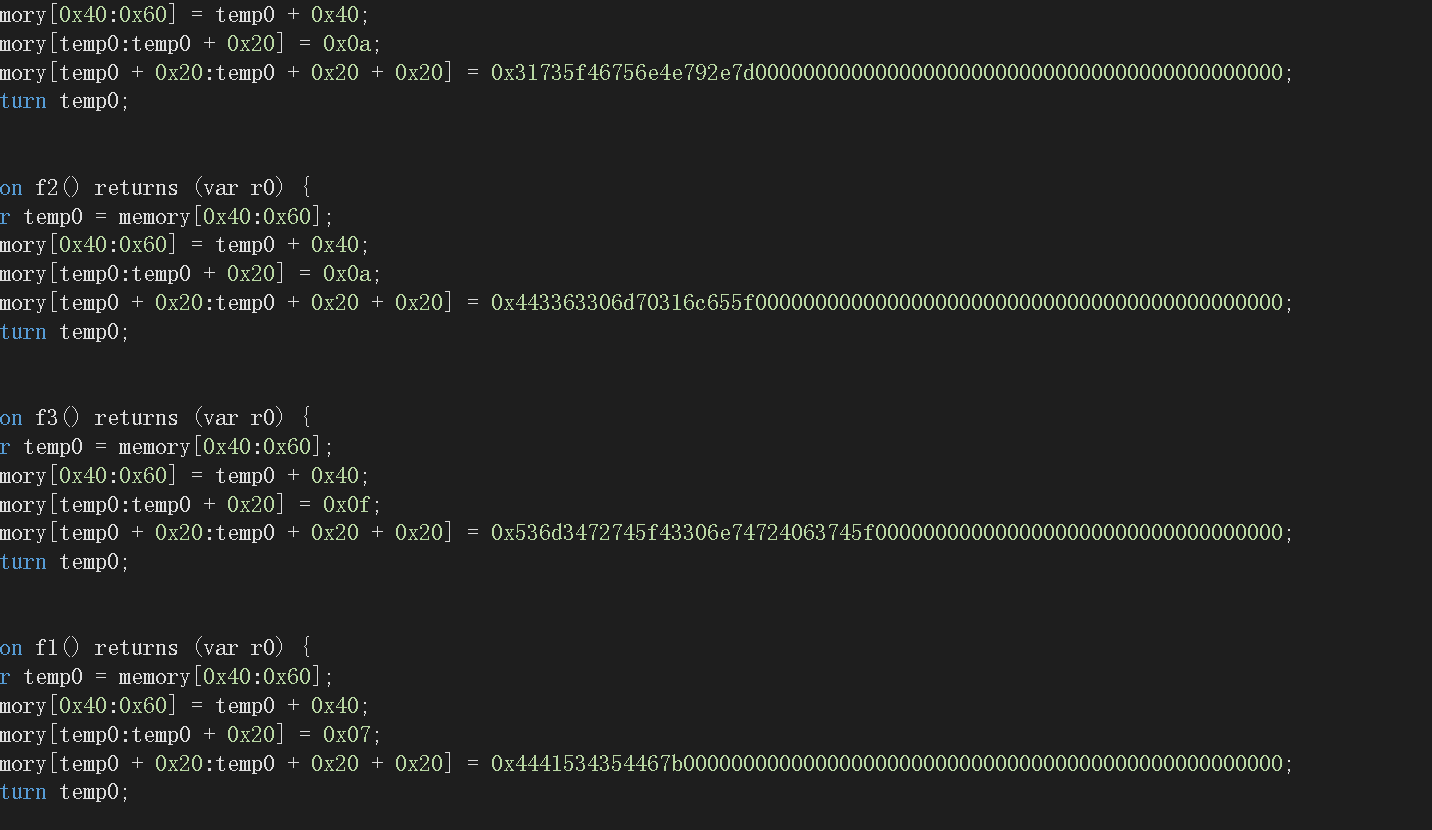

5.发现顺序是乱的，以我神级英语水平，大概的顺序就是:’反编译智能合约字节码真的不错’,hhhhhhhhhhhh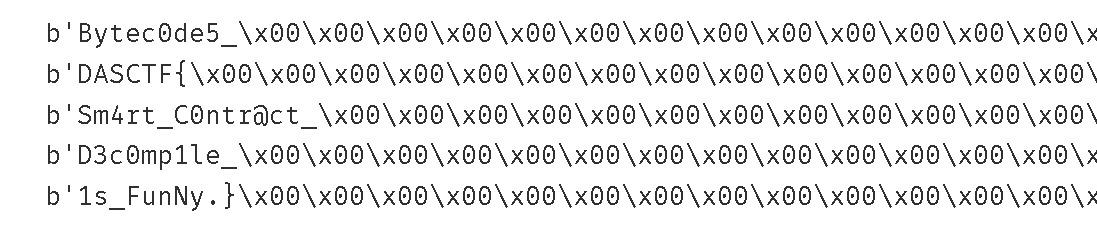

from Crypto.Util.number import *

print(long_to_bytes(0x4279746563306465355f00000000000000000000000000000000000000000000))
print(long_to_bytes(0x4441534354467b00000000000000000000000000000000000000000000000000))
print(long_to_bytes(0x536d3472745f43306e74724063745f0000000000000000000000000000000000))
print(long_to_bytes(0x443363306d70316c655f00000000000000000000000000000000000000000000))
print(long_to_bytes(0x31735f46756e4e792e7d00000000000000000000000000000000000000000000))
# DASCTF{D3c0mp1le_Sm4rt_C0ntr@ct_Bytec0de5_1s_FunNy.}

赛后复现密码—–逆向第三道懒得复现，还有密码第三道。。。。。。==看了一遍代码就把文件扔到回收站了==

easy_Affline

这道题题目给的a，b数字太大，我以为要爆破很长的区间，其实不用，经过我脚本的测试，发现大数字和小数字的结果是相同的，所以只需遍历0~m即可

from Crypto.Util.number import *
import random
text = 'aCdhpnlmNKuRJbfVIXUvyTrSPqjBMzgwHZkAxWGiYetEsocDLFOQ'
cipher = 'CezmBh{BKDdD_oP_rKD_rdtF_cMHu}'
flag='DASCTF'
i = 0

def d():
    for a in range(2, 52):
        
        for b in range(2, 52):
            if GCD(a,52) == 1:
                break
            c = ''
            t = inverse(a,52)
            for i in cipher:
                x = text.find(i)
                c += text[t*(x-b) % len(text)]
            if c == flag:
                print(a,b)
                return
        
d()
a = 2
b = 6
t = inverse(a,52)
flag = ''
for i in cipher:
        if i not in text:
            flag += i
        else:
            x = text.find(i)
            flag += text[t*(x-b) % len(text)]
print(flag)
# DASCTF{TheLe_iU_Ihe_ILxE_Yrjp}

gauss_system

sage解即可

k = 1751007263671615053487807501173970925758538
c = 463982900309034681135307002234842926080979
p, q = var("p, q")
assume(p, "integer")
assume(q, "integer")
sol = solve((p - 1003) ** 2 + (q - 48) ** 2 == k, p, q)

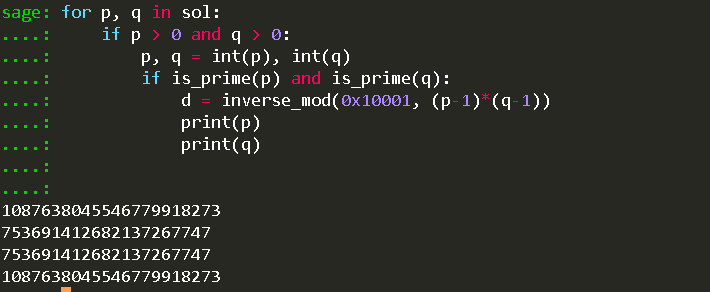
for p, q in sol:
    if p > 0 and q > 0:
        p, q = int(p), int(q)
        if is_prime(p) and is_prime(q):
            print(p)
            print(q)

import libnum
import gmpy2
from Crypto.Util.number import *
e = 0x10001
s = 1751007263671615053487807501173970925758538
c = 463982900309034681135307002234842926080979
p = 1087638045546779918273
q = 753691412682137267747
assert p**2 + q**2 == s
phi = (p-1)*(q-1)
d = libnum.invmod(e,phi)

n = p*q
m = pow(c,d,n)
long_to_bytes(m)
# Z[i]_15_m4g1c

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论，也可以邮件至 jaytp@qq.com