学习一下csapp,第一篇
在32位系统:-2147483648 < 2147483647 结果为false
int i = -2147483648; i < 2147483647 结果为true
-2147483648-1 < 2147483647 结果为true
在计算机中运算是会发生溢出,假如运算后的数超过了32位,那最终结果可能是一个负数,或者是其他正整数
我们用linux中的gdb软件来证明其中的结论
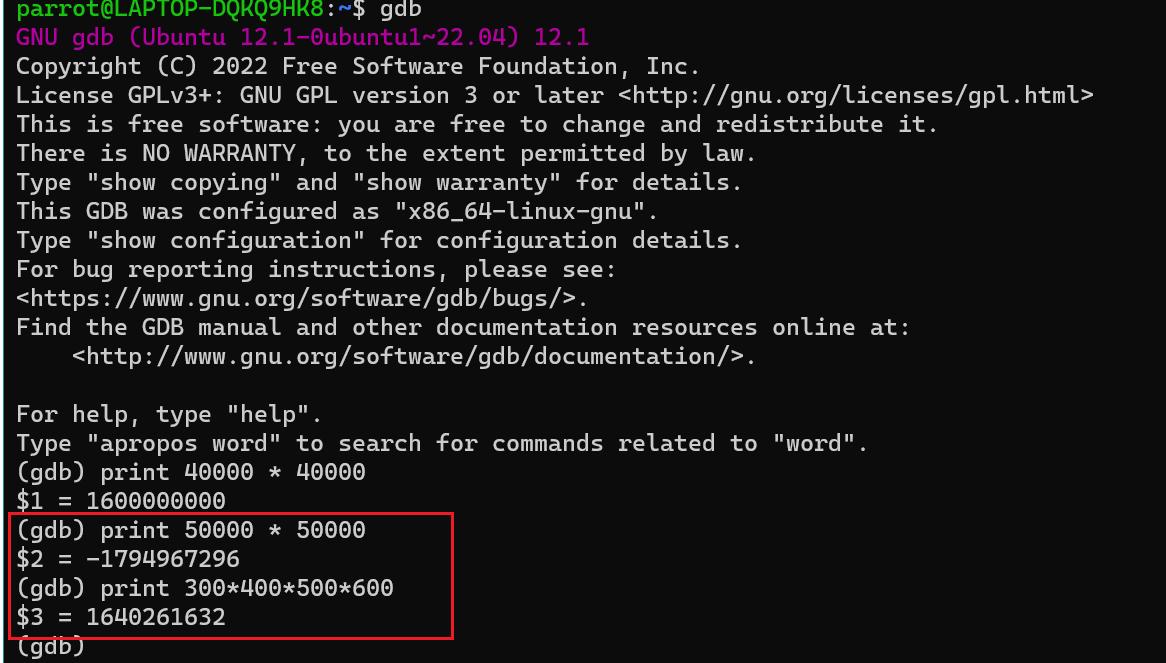
很显然,上述超乎我们的预想
然而在整数运算时是符合交换律的,但是在计算机中浮点数却不符合交换律
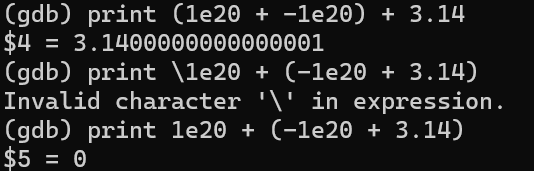
这里做一个实验:用(1e20 + -1e20) + 3.14
结果为:3.1400000000000001
再用1e20 + (-1e20 + 3.14),这里3.14对于-1e20微不足道
结果为:0
他们用有限的位组合形式表示在数域中无线扩张的数
定点数和浮点数
计算机中只能通过约定小数点的位置来表示
- 小数点位置约定在固定位置的数称为定点数
- 小数点位置约定为可浮动的数称为浮点数
- 定点小数用来表示浮点数的尾数部分
- 任何实数:X=(-1)^s^ ×M×R^E^
其中,S取值为0或1,用来决定数X的符号;M是一个二进制定点小数 ,称为数X的尾数(mantissa);E是一个二进制定点整数,称为数X 的阶或指数(exponent);R是基数(radix、base),可以为2、4和16等,计算机中只要表示S、M和E三个信息,就能确定X的值,叫浮点数
定点数的编码表示
浮点数(可用一个定点小数和一个定点整数来表示)
定点数的编码(解决正负号问题): 原码、补码、移码、反码 (很少用)
原码表示:
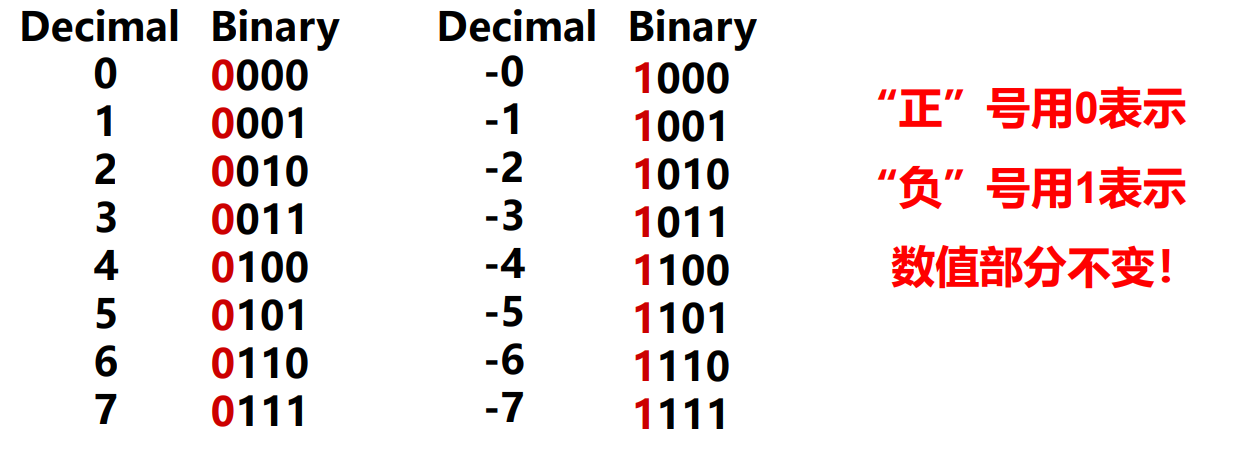
- 其中由上图得0有两种表示,不唯一
- 加减方式,对于同号,取绝对值相加,然后在加上符号,对于异号,是比较哪个绝对值大,然后大的间小的,然后再加上绝对值大的符号。这样加减方式繁琐不统一
==从 50年代开始,整数都采用补码来表示 但浮点数的尾数用原码定点小数表示==
补码 - 模运算(modular运算)
在一个模运算系统中,一个数与它除以“模”后的余数等价
一个负数的补码等于模减该负数的绝对值
对于某一确定的模,某数减去小于模的另一数,总可 以用该数加上另一数负数的补码来代替
补码(modular运算):+ 和– 的统一
例1:“钟表”模运算系统 假定时针只能顺拨,从10点倒拨4格后是几点?
10- 4 = 10+(12- 4) = 10+8 = 6(mod 12)

结论:一个负数的补码等于将对应正数补码 各位取反、末位加一
补码的定义 假定补码有n位,则:[X]补= 2n + X (-2n-1≤X<2n-1 ,mod 2n)
X是真值,[x]补是机器数
求特殊数的补码
假定机器数有n位:
① [-2^n-1^]补= 2^n^ - 2^n-1^ = 10…0(n-1个0) (mod 2^n^)
② [-1]补= 2^n^ - 0…01 = 11…1(n个1) (mod 2^n^)
③ [+0]补= [-0]补= 00…0(n个0)
变形补码的表示
变形(4’s)补码:双符号,用于存放可能溢出的中间结果
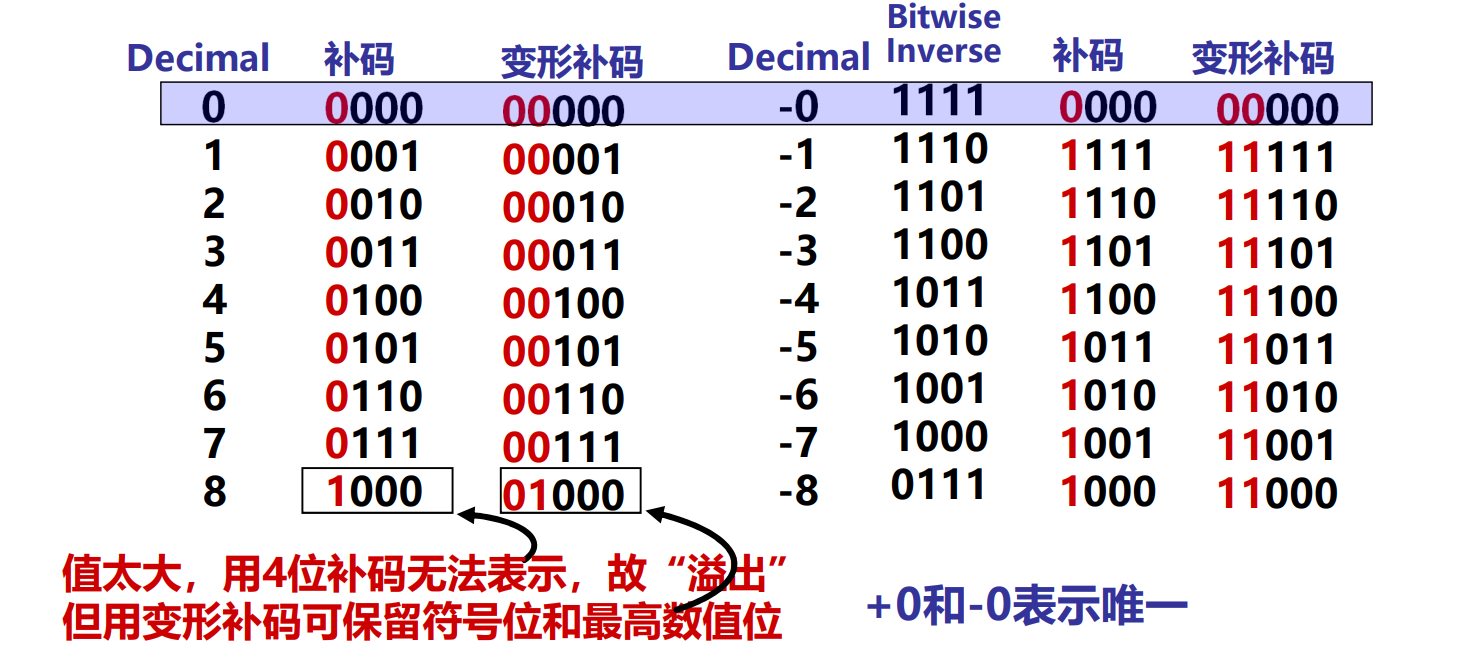
求真值的补码:
简便方法:从右向左遇到第一个1的前面各位取反
求补码的真值:
简便求法: 符号为0,则为正数,数值部分相同 符号为1,则为负数,数值各位取反,末位加1

移码表示Excess
- 什么是移码表示?
- 将每一个数值加上一个偏置常数( Excess / bias)
- 通常,当编码位数为n时,bias取 2^n-1^ 或 2^n-1^-1(如 IEEE 754)

- 为什么要用移码来表示指数(阶码)?
- 便于浮点数加减运算时的对阶操作(比较大小)

带符号整数
有三种定点编码方式:
- Signed and magnitude (原码):定点小数,用来表示浮点数的尾数
- Excess (biased) notion (移码):定点整数,用于表示浮点数的阶(指数)
- Two’s complement (补码):50年代以来,所有计算机都用补码来表示带符号整数
为什么用补码表示带符号整数?
- 补码运算系统是模运算系统,加、减运算统一
- 数0的表示唯一,方便使用
- 比原码多表示一个最小负数
无符号数:常在一个数的后面加一个“u”或“U”表示无符号数
==若同时有无符号和带符号整数,则C编译器将带符号整数强制转换为无符号数==
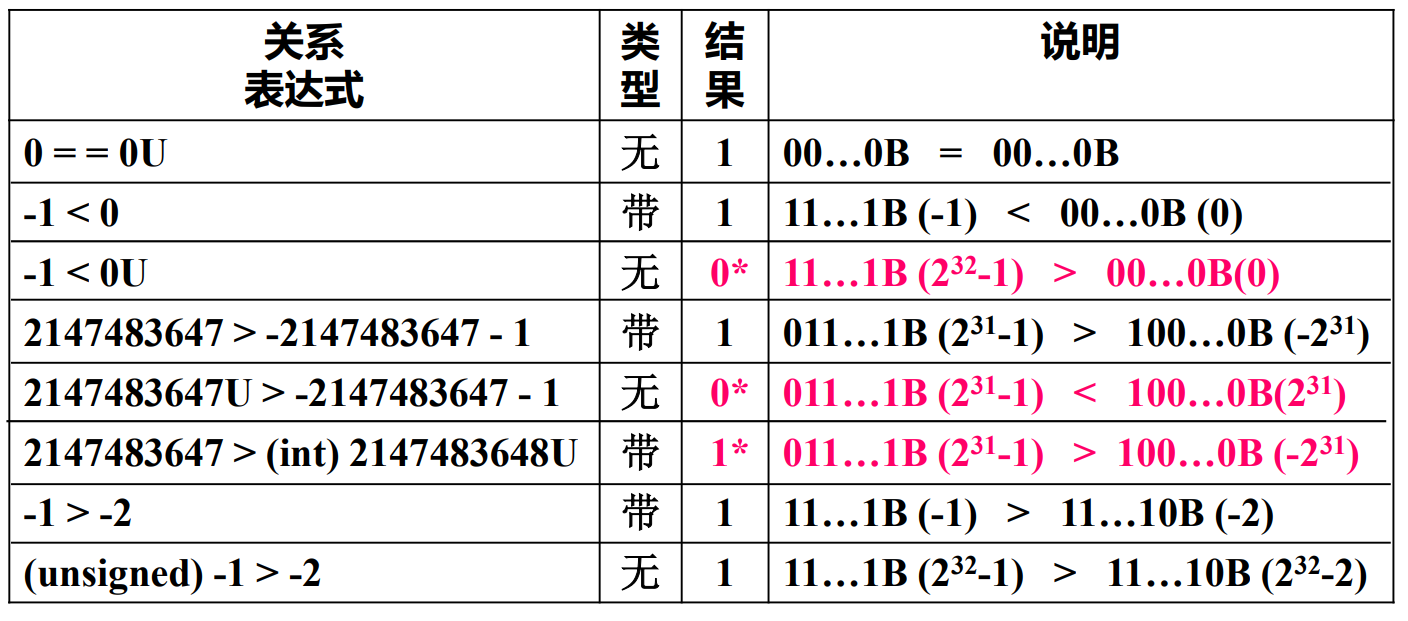
带*的与预想的不同

编译器处理常量时默认的类型
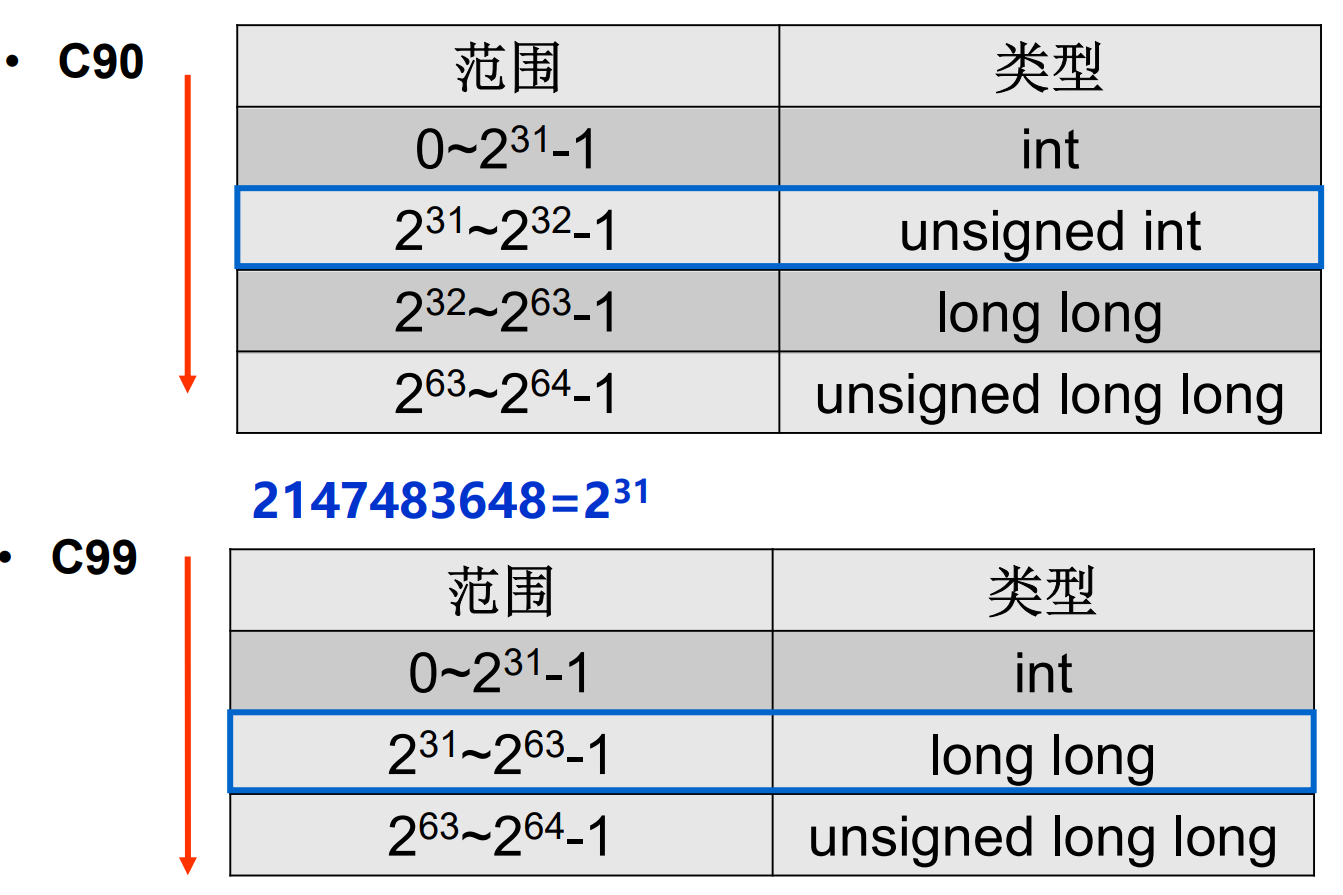
C表达式-2147483648 < 2147483647的执行结 果为false,这是因为编译器在编译时,是把符号和字面量分开识别,先识别字面量2147483648,2147483648在C90中时2^31^,属于unsigned int,所以此次比较是根据无符号数来进行比较。
若定义变量“int i=-2147483648;”,则“i < 2147483647”的执行 结果为true,这个不用解释,int类型已经定义好类型了,不需要再判别
如果将表达式写成“-2147483647-1 < 2147483647”,则结果会怎 样呢?是true
不过C99的标准不一样,看上面的表就知道
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 jaytp@qq.com

