question: double
PAT甲级题
给定一个正数数列,我们可以从中截取任意的连续的几个数,称为片段。例如,给定数列 { 0.1, 0.2, 0.3, 0.4 },我们有 (0.1) (0.1, 0.2) (0.1, 0.2, 0.3) (0.1, 0.2, 0.3, 0.4) (0.2) (0.2, 0.3) (0.2, 0.3, 0.4) (0.3) (0.3, 0.4) (0.4) 这 10 个片段。
给定正整数数列,求出全部片段包含的所有的数之和。如本例中 10 个片段总和是 0.1 + 0.3 + 0.6 + 1.0 + 0.2 + 0.5 + 0.9 + 0.3 + 0.7 + 0.4 = 5.0。
输入格式:
输入第一行给出一个不超过 105 的正整数 N,表示数列中数的个数,第二行给出 N 个不超过 1.0 的正数,是数列中的数,其间以一个空格分隔。
输出格式:
在一行中输出该序列所有片段包含的数之和,
输入样例:
4
0.1 0.2 0.3 0.4
输出样例:
5.00
关于这题的分析:
我是看了柳神的,我天真地以为一个数据出现了n-1词,但比如0.2在0.1的条件下,就已经出现了3次了
柳神原话:将数列中的每个数字读取到temp中,假设我们选取的片段中包括temp,且这个片段的首尾指针分别为p和q,那么对于p,有i种选择,即12…i,对于q,有n-i+1种选择,即i, i+1, … n,所以p和q组合形成的首尾片段有i * (n-i+1)种,因为每个里面都会出现temp,所以temp引起的总和为temp * i * (n – i + 1);遍历完所有数字,将每个temp引起的总和都累加到sum中,最后输出sum的值
原先的代码:
#include<iostream>
using namespace std;
int main(void){
int n;
double tmp,sum = 0;
cin >> n;
for(int i=0;i<n;i++){
cin >> tmp;
sum += tmp * (i + 1) * (n - i);
}
printf("%.2f",sum);
return 0;
}
结果不太行啊
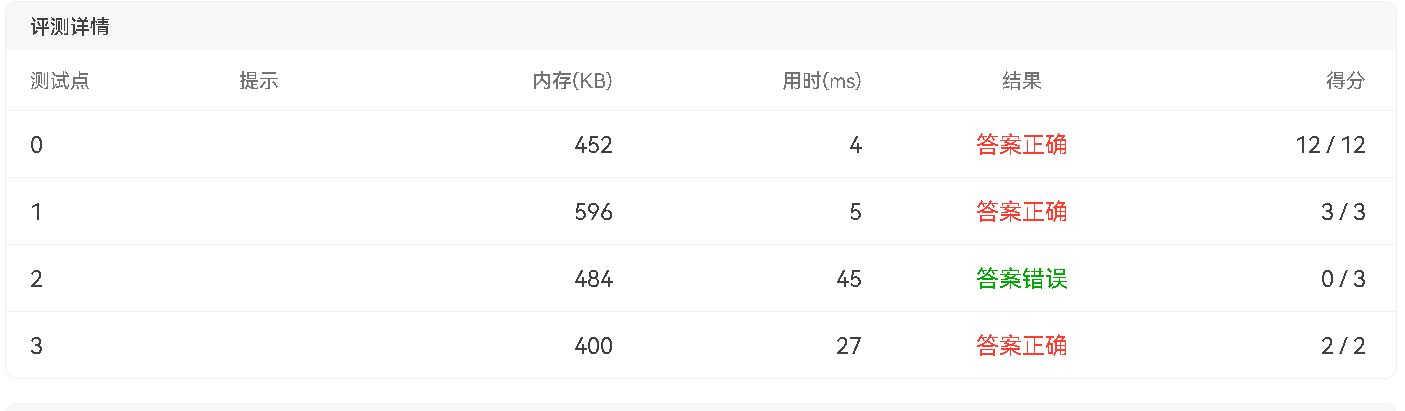
这里用double进行运算时是会产生误差的,因为有些数用二进制表示不出来,c++中只能粗略表示.
具体参考文章:由一道 OJ 引发的关于 double 类型的一些思考 | Lust for Life (bipy.me)
然后大佬给出的方案是用long long 类型进行小数点后移×1000,这里其实就要考虑所给的数据是否都是最多小数点后三位了
#include<iostream>
using namespace std;
int main(void){
int n;
long long sum = 0;
double tmp;
cin >> n;
for(int i=0;i<n;i++){
cin >> tmp;
sum += (long long)(tmp * 1000) * (i + 1) * (n - i);
}
printf("%.2f",sum/1000.0);
return 0;
}
然后这里居然才4.99
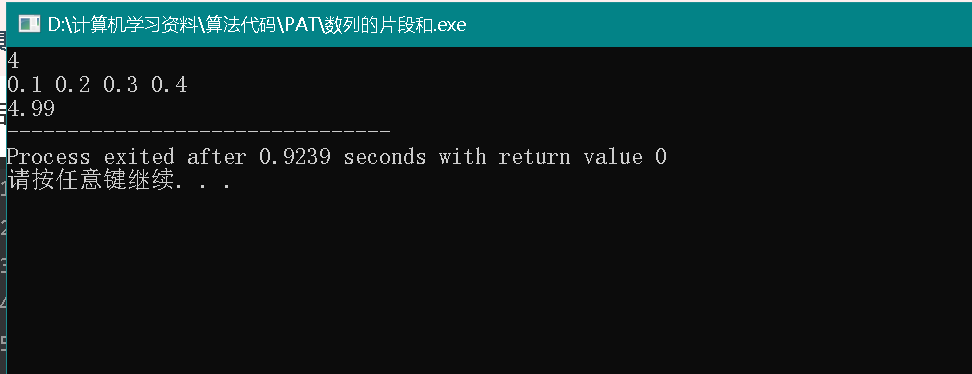
更离谱的是给通过了😂笑死,反正我感觉很不靠谱
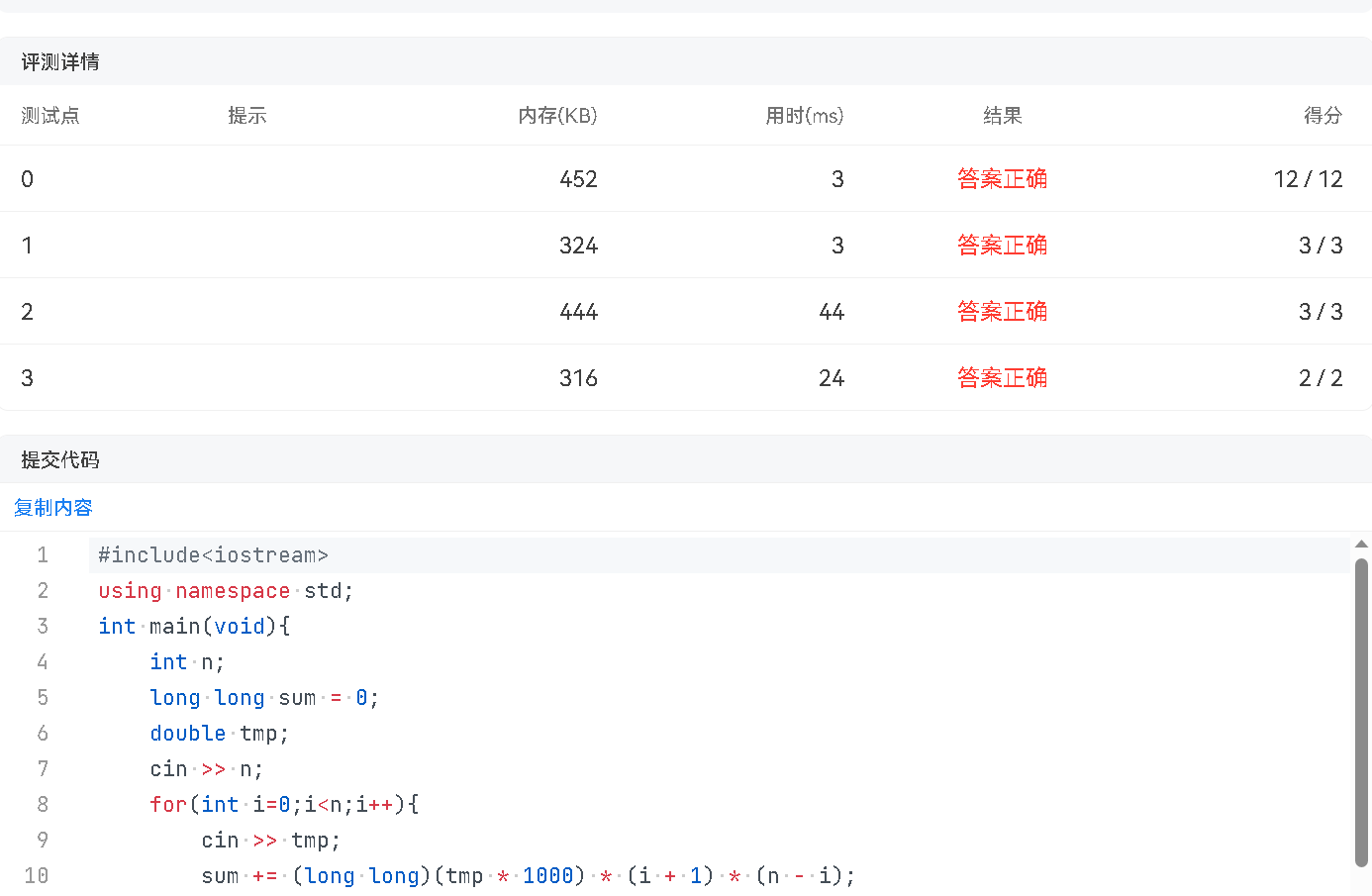
其实我觉得这题用java中的bigdecimal才是最优
动态规划类解法:(从后往前遍历)
#include<iostream>
using namespace std;
int main(void){
int n;
double tmp;
long long sum = 0;
cin >> n;
long long seq[n];
for(int i=0;i<n;i++) {
cin >> tmp;
seq[i] = (long long)(tmp * 1000);
}
sum = seq[n-1];
for(int i=n - 2;i !=-1 ;i--){
seq[i] = seq[i] * (n - i ) + seq[i+1];
sum += seq[i];
}
printf("%.2f",sum/1000.0);
return 0;
}
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 jaytp@qq.com

